对于任何数据岗位相关的面试，Python编程是一项必要技能，因此它也是面试中必须去准备的一环！今天就和大家一起讨论几个Python经典题目。

这类面试中大多会包括四类编程问题：数据结构和算法（Data Structure and Algorithm），机器学习算法（Machine Learning Algorithms），数学统计（Math and Statistics）和数据处理（Data Manipulation）。

我曾在相关文章中对数据处理（Data Manipulation）与字符串提取（String Extraction）这两个主题进行过详述。而今天的文章，我会着重从数学（Math）与统计学（Statistics）的角度出发，对一些大型科技公司（尤其是FAANG）提出过的五大Python编程问题进行代码详解。这类问题通常会给为你提供一个商业环境（Business setting），然后要求你通过模拟（simulations）的方式来提供一个统计学上的解答。

问题1：谁先赢？（微软Microsoft）

Amy 和 Brad轮流掷一个六面骰子（骰到任意一面概率相同）。谁先掷出“6”，谁就获胜。Amy 先掷。那么请问Amy 获胜的几率是多少？

我的思路：

这是一个典型的模拟问题，最好的解决方法就是大批量模拟该过程来获取Amy的获胜概率。

由Amy先掷。如果结果是6，那么游戏结束，Amy获胜。否则就轮到Brad掷。如果Brad掷到6，Brad获胜。如果这时游戏还未结束，就继续由Amy投掷。重复这个过程，直到有人掷出6时游戏结束。

这里的关键是要充分理解整个逻辑流程：谁赢了，并且是在什么情况下获胜的。如果Amy掷到了6，Brad还需要继续游戏吗？答案是否定的。

代码：

注意第六行：A_6是Amy的数据分布，如果她的游戏结果为6，那么她的计数器就+1。若不是，换由Brad掷骰子。

在代码的末尾，程序的最终结果应该是用Amy获胜的次数除以Amy和Brad获胜次数的总和。这里的一个常见错误是会用A_count除以模拟的总数来获得结果，但这是不正确的。因为模拟的总次数也包括了Amy和Brad都未能掷出6的情况。

让我们来验证一下上述代码。

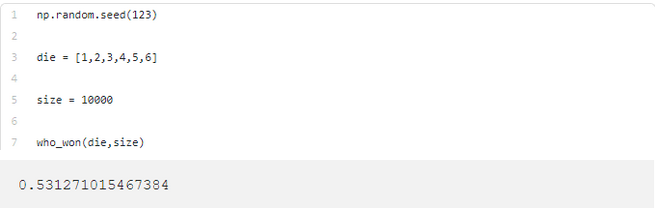
代码结果表明：Amy在这场游戏中占了上风，因为她先于Brad开始掷筛子。在10,000次模拟中，Amy的获胜概率为53％。

问题2：6 和9组成的最大数字（各大公司常见题）

• 给定一个仅由数字6和9组成的正整数（positive integer）。
• 在仅仅修改一位数字的情况下输出最大数值（由6变成9或者9变成6）。
• https://leetcode.com/problems/maximum-69-number/

我的思路：

对于一个正整数，只需要考虑一种方法来增大它的值，那就是把“ 6”变成“ 9”。同时，我们必须改变尽量靠左的6。否则输出结果就不会是最大值。举例来说，我们必须将“6996 ”改为“9996”以获得最大值，而不是“6999 ”。

我为这个问题提出了两种题目的变体：替换一个6，或者替换全部6。

变体1：替换一个6

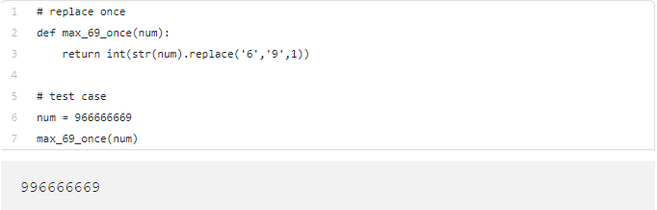
在第3行，我们先将整数转换为字符串，然后将第一个“ 6”替换为“ 9”，最后使用int()把它还原为整数。

变体2：替换全部6

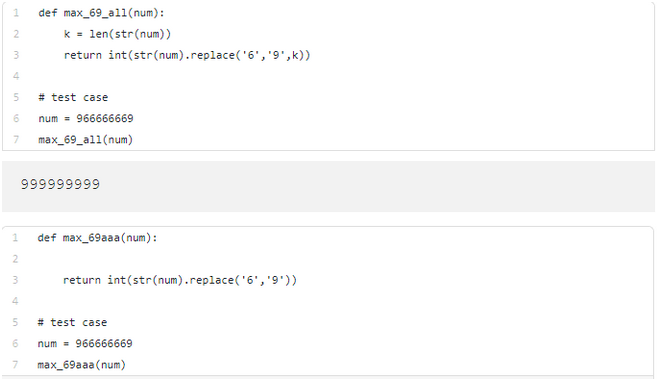
关于变体2的解题代码，我们其实不需要指定变量k的值，因为replace()方法会默认替换全部适配的值。在这里，我定义k值仅仅是为了演示目的。这个问题还有可能的变体，是要求答题者替换数字的前两个或三个“6”，来使数字最大化。

问题3：有效的完全平方数（Facebook）

• 给定一个正整数（positive integer）。编写一个函数，返回输入的正整数是否是一个完全平方数。
• 后续问题：不使用任何内置的库函数（built-in library function），比如sqrt函数。
• https://leetcode.com/problems/valid-perfect-square/

我的思路：

思路非常直接：检查这个正整数是否有完全平方根（perfect square root）。如果有，就返回True。这可以分为两步完成：

• 1、求平方根（square root）
• 2、检查是否为完全平方根（perfect square root）

需要注意的是，如果我们使用一些内置库（built-in library）提供的函数（例如，math，Numpy）来计算平方根，那么在LeetCode上它就只是一个简单级别的问题。但如果我们不使用这些内置库，那它就会是一个中等级问题。

方案1：使用内置库

这个算法可以轻松通过所有测试案例。在这里，我们使用了int()函数来截取平方根的整数部分。对于完全平方这不会造成任何区别，等式依旧成立。而对于非完全平方，等式不成立，返回结果False。

方案2：不使用内置库（built-in library）— 二分查找（binary search）

如果不使用内置库，我们可以使用二分查找（binary search）。LeetCode上有很多关于二分查找的详解(https://leetcode.com/problems/valid-perfect-square/solution/)。

简单来说：我们创建左右两个指针，并比较原数字与这两个指针指向数字的平均值（average value）。如果它小于原数，就增加它的值;如果是大于，我们就减少它的值;如果相等，就返回True。

我们使用while循环（while loop）来对这些情况进行自动检查。

问题4：阶乘后的零

（Factorial Trailing Zeroes）（Bloomberg）

• 给定一个整数 n，返回 n! 结果末尾中零的数量
• 后续问题: 你能提供一个log时间复杂度（logarithmic time complexity）的解决方案吗？
• https://leetcode.com/problems/factorial-trailing-zeroes/

我的思路

共分为两步：

• 1、计算n的阶乘（factorial）n!
• 2、计算尾数中零（ trailing zeroes）的数量

第一步相对简单，我们使用while循环（while loop）对n的阶乘进行迭代（iteratively loop）直到数字1。但第二步有点棘手。

这个问题要求的是末尾0的数量，而不是总共0的数量。这区别很大。比如8 !的结果是40320，它包含2个0，但它的末尾只有1个0。所以我们在计算时必须格外小心。我一共提出了两种解决方案。

方案1：反向读取字符串（string）

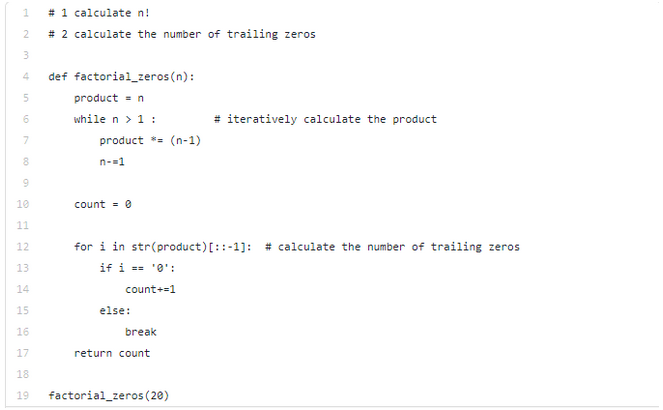
第一部分计算阶乘的代码一目了然。第二部分，我们先使用str()方法将结果转换为一个字符串，然后反向读取:如果数字为0，就在计数器加1;否则，我们就跳出循环。

这里必须使用到break命令。如不使用break，代码会计算所有零的总数。

方案2：while循环（While Loop）

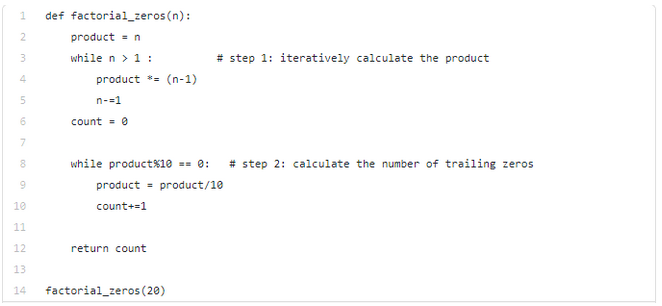
这个方案计算阶乘的部分与方案1相同，唯一的区别是，我们使用while循环来计算末尾0的数量：对于可以被10整除的乘积，其最后一位数字必须是0。因此，我们使用while循环来不断更新循环条件，直到条件不再成立。

顺带一提，方案2也是我最喜欢的计算末尾零个数的方法。

问题5：完美数（Perfect Number）（亚马逊Amazon）

• 对于一个正整数，如果它和除了它自身以外的所有正因子的和相等，我们称它为完美数
• 给定一个整数n，返回它是否是完美数
• https://leetcode.com/problems/perfect-number/

我的思路可以分为三步：

• 1、找出正因子
• 2、计算总和
• 3、判断是否是完美数

第2步和第3步相对简洁明了，最多不超过一行代码。困难的部分是如何找到正因数。在这里，我们采用蛮力（brutal force）法在1到正整数的整个区间内进行查看。

理论上，这个方法会对较小的整数有效。如果我们输入一个较大的数字，很有可能会超时。

方案1：蛮力（brutal force）法

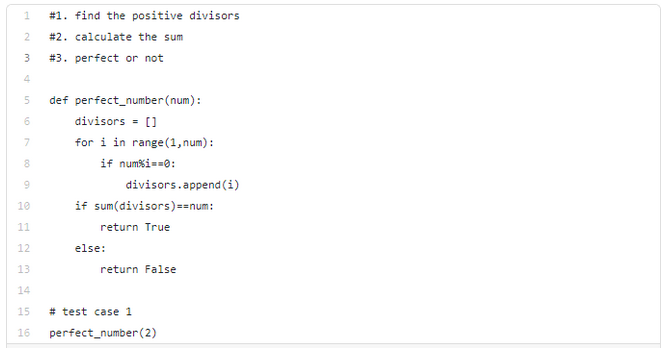
这种方法并不适用于较大的输入值。你的面试官很有可能会要求你提供一个更有效率的解决方案。

方案2：sqrt(n)

找因数并不需要查看从1到输入数字之间的全部整数。比如说，要找出100的因数，我们不需要查看从1到100之间的所有的整数。其实，我们只需要遍历到100的平方根(即10)，所有的可能因数就已经包含在内了。这一方法可以节省大量计算时间。

要点总结：

• 在进行了数十次实战编程之后，你会发现最重要的一个要点，就是需要理解问题，并把问题拆分成多个可操作的部分。
• 在这些被拆分的部分中，总会有一个部分是相对困难的。并且它们经常会伴有“不能使用内置库函数”等限制。
• 要克服这些困难，你需要在平日的练习中就尽量避免使用内置库函数，自己练习编写逻辑清晰的函数来替代相关功能。

感谢你的阅读！

原文作者：Leihua Ye
翻译作者：Lea
美工编辑：过儿
校对审稿：Jiawei Tong
原文链接：https://towardsdatascience.com/5-python-coding-questions-asked-at-faang-59e6cf5ba2a0